Boyutlar Arası İlişkiler:
KÜP:
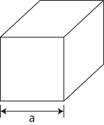
Hacim
\(V = {a^3}{\rm{ }}\)
Yüzey Alanı \({{\rm{S}}_{\rm{Y}}}{\rm{ = 6}}{{\rm{a}}^{\rm{2}}}\)
Kesit Alanı \({{\rm{S}}_K}{\rm{ = }}{{\rm{a}}^{\rm{2}}}{\rm{ }}\)
\(\frac{{{\rm{Yüzey Alan\imath }}}}{{{\rm{Hacim}}}}{\rm{ = }}\frac{{{\rm{6}}{{\rm{a}}^{\rm{2}}}}}{{{{\rm{a}}^{\rm{3}}}}}{\rm{ = }}\frac{{\rm{6}}}{{\rm{a}}}\)
\(\frac{{{\rm{Kesit Alan\imath }}}}{{{\rm{Hacim}}}}{\rm{ = }}\frac{{{{\rm{a}}^{\rm{2}}}}}{{{{\rm{a}}^{\rm{3}}}}}{\rm{ = }}\frac{{\rm{1}}}{{\rm{a}}}\)
Hacim \(V = abc{\rm{ }}\)
Yüzey Alanı \({S_Y} = 2(ab + bc + ac)\)
Kesit Alanı \({S_K} = ab\)
\(\frac{{Yüzey{\rm{ Alan\imath }}}}{{Hacim}} = \frac{{2(ab + bc + ac)}}{{abc}}\)
\(\frac{{Kesit{\rm{ Alan\imath }}}}{{Hacim}} = \frac{{ab}}{{abc}} = \frac{1}{c}\)
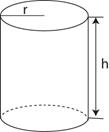
Hacim \(V = \pi {r^2}h\)
Yüzey Alanı \({S_Y} = 2\pi {r^2} + 2\pi rh\)
Kesit Alanı \({S_K} = \pi {r^2}\)
\(\frac{{Yüz.{\rm{ A}}{\rm{.}}}}{{Hacim}} = \frac{{2\pi {r^2} + 2\pi rh}}{{\pi {r^2}h}} = \frac{{2(r + h)}}{{rh}}\)
\(\frac{{Kesit{\rm{ Alan\imath }}}}{{Hacim}} = \frac{{\pi {r^2}}}{{\pi {r^2}h}} = \frac{1}{h}\)
KÜRE:
Hacim \(V = \frac{4}{3}\pi {r^3}\)
Yüzey Alanı \({S_Y} = 4\pi {r^2}\)
Kesit Alanı \({S_K} = \pi {r^2}\)
\(\frac{{Yüzey{\rm{ Alan\imath }}}}{{Hacim}} = \frac{{4\pi {r^2}}}{{\frac{4}{3}\pi {r^3}}} = \frac{3}{r}\)
\(\frac{{Kesit{\rm{ Alan\imath }}}}{{Hacim}} = \frac{{\pi {r^2}}}{{\frac{4}{3}\pi {r^3}}} = \frac{3}{{4r}}\)
Çıkan Sonuçlar:
Bir cismin boyutları hangi oranda değişirse, kesit alanı bu oranın karesi ile orantılı değişir.
Bir cismin boyutları hangi oranda değişirse, hacmi bu oranın kübüyle orantılı değişir.
Bir cismin boyutları hangi oranda değişirse, ağırlığı ve kütlesi hacmindeki değişim kadar değişir.
Cisimlerin boyutları büyürken,\(\frac{{Kesit{\rm{ Alan\imath }}}}{{Hacim}}\) ve \(\frac{{{\rm{Yüzey Alan\imath }}}}{{Hacim}}\) oranı azalır.
Bir cismin boyutları hangi oranda değişirse, yüzey alanı bu oranın karesi ile orantılı değişir.
Dayanıklılık
Bir maddenin üzerindeki bir yükü ya da kuvveti taşıyabilme özelliğidir.
\({\rm{Dayan\imath kl\imath l\imath k = }}\frac{{{\rm{kesit alan\imath }}}}{{{\rm{ag\imath rl\imath k}}}}{\rm{\alpha }}\frac{{{\rm{kesit alan\imath }}}}{{{\rm{hacim}}}}\)
– Bir cismin dayanıklılığı, boyut değiştirme oranı ile ters orantılıdır. Yani boyut artarsa dayanıklılık azalır, boyut azalırsa dayanıklılık artar.
Boyutları 2 katına çıkarılan bir cismin dayanıklılığı yarıya iner.
– Canlının kaybettiği ısı enerjisi, canlının yüzey alanı ile doğru orantılıdır.
Filin birim zamanda kaybettiği ısı kedininkinden fazladır.
– Canlının tükettiği minimum besin miktarı, canlının yüzey alanı ile doğru orantılıdır.
Filin hayatta kalabilmesi için yemesi gereken minimum besin kedininkinden fazladır.
– Bir canlının boyutları aynı oranda azaltılırsa yüzey alanının hacime oranı artar. Böylece tükettiği besin miktarının ağırlığa oranı artar.
Farelerin aç ve huzursuz olmalarının nedeni budur.
Doğada fareden daha küçük sıcak kanlı hayvanın yaşayamaması aynı nedene dayanır.