Yansıtıcı yüzeyi küre parçası olan aynalara denir. Küresel aynalar iki şekilde incelenir. Yansıtıcı yüzeyi, küre parçasının iç yüzeyi ise çukur ayna ya da içbükey ayna (konveks ayna ) denir. Eğer yansıtıcı yüzeyi küre parçasının dış yüzeyi ise tümsek ayna ya da dış bükey ayna ( konkav ayna ) denir.
ÇUKUR AYNA
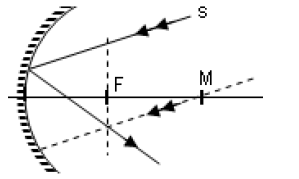
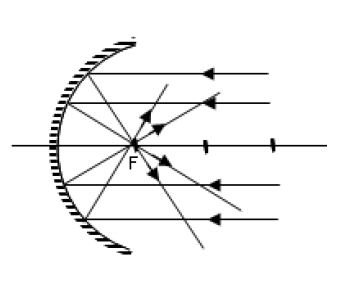
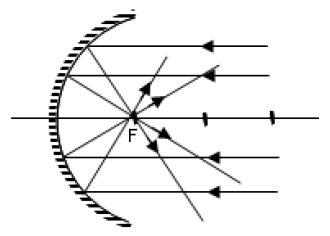
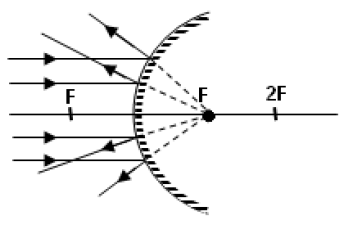
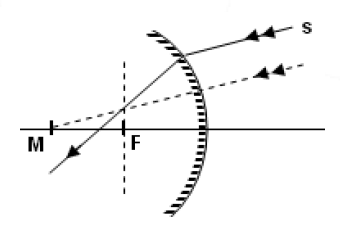
Yansıtıcı yüzeyi, küre parçasının iç yüzeyi ise çukur ayna ya da içbükey ayna ( konveks ayna ) denir. Çukur aynaların toplayıcı özelliği vardır. Bu aynalar güneş ışınlarına dik tutulursa, ışınlar yansıdıktan sonra bir noktada kesişirler. Bu noktaya aynanın odak noktası denir ve F ile gösterilir.
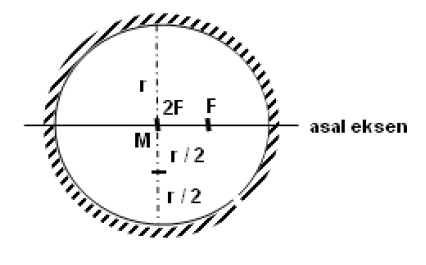
Aynanın merkezi M ile gösterilir ve aynı zamanda aynanın yarıçapına eşittir.
\(M = r = 2F\)
\(F = \frac{M}{2}\)
Çukur aynada özel ışınlar:
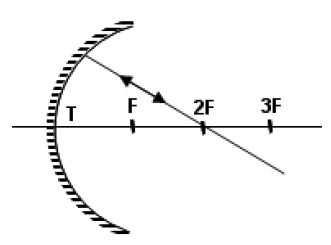
Çukur aynaya paralel gelenler ışınlar odaktan geçecek şekilde yansır. Aynı zamanda odaktan gelen ışınlar da paralel yansır.
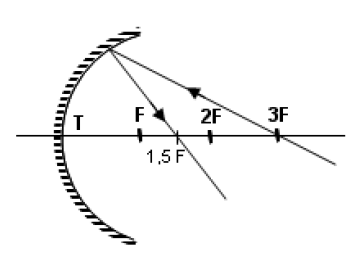
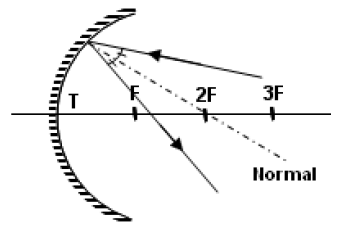
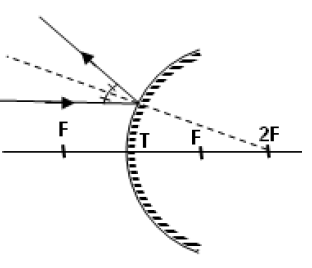
Çukur aynaya 3F noktasını keserek gelen ışın 1,5 F‘den geçecek şekilde yansır. Aynı zamanda 1,5 F den gelen ışında 3F’ den geçecek şekilde yansır.
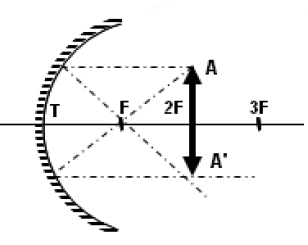
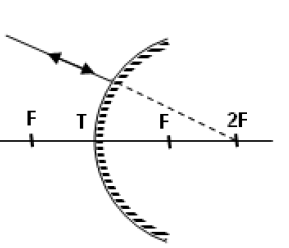
Çukur aynaya merkezden ( 2F ) gelen ışınlar kendi üzerinden geri yansır.
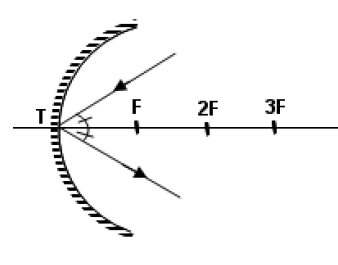
Çukur aynanın tepe noktasına gelen ışın asal eksenle eşit açı yapacak şekilde yansır.
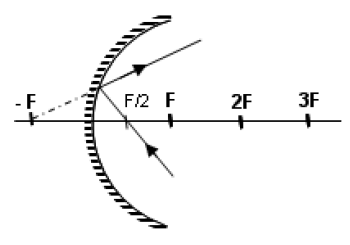
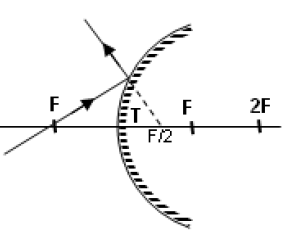
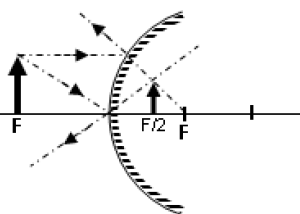
Çukur aynaya 0,5F‘den gelen ışınlar F‘den geçecek şekilde yansır.
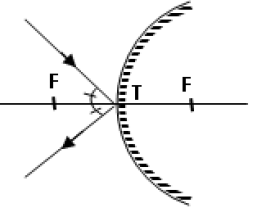
Çukur aynaya rastgele gelen bir ışın aynanın normali olan merkezden gelen çizgiyle eşit açıyla yapacak şekilde yansır.
Yardımcı odak yardımıyla yansıyan ışının çizilmesi;
Aynaya paralel gelen ışın demeti asal eksene paralel değilse de yansıyan ışınların kendileri ya da uzantıları asal eksen üzerinde bulunmayan bir noktadan geçer bu noktaya Yardımcı odak denir.
Yansıyan ışını çizmek için;
- Merkezden geçen ve gelen ışına paralel olan yardımcı bir eksen çizilir.
- Asal eksene dik olan ve odaktan geçen odak düzlemi çizilir.
- İki eksenin kesiştiği nokta yardımcı odaktır ve yansıyan ışın bu noktadan geçer.
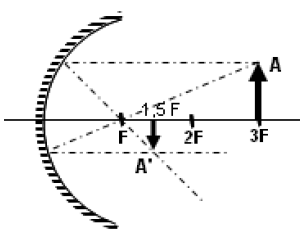
Çukur aynada görüntü
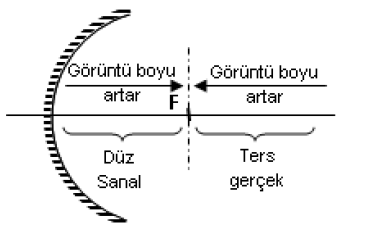
Bir cismin aynadaki görüntüsünü çizme için, cisimden aynaya en az iki ışın gönderilir. Bu ışınların yansıdıktan sonra kesiştikleri yerde görüntü oluşur. Eğer yansıyan ışınların kendisi kesişiyorsa görüntü gerçek, yansıyan ışınların kendisi değilde uzantısı kesişiyorsa görüntü sanaldır.
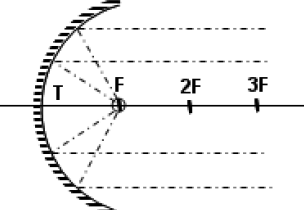
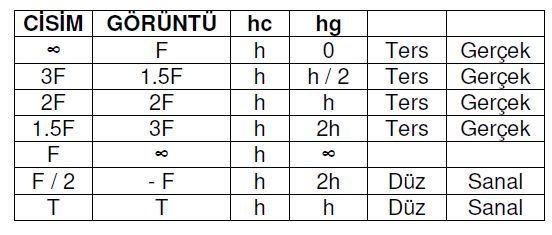
- Sonsuzdaki bir cismin çukur aynada görüntüsü aynanın odağındadır ve görüntü noktasaldır.
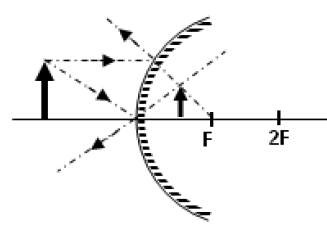
- Çukur aynada 3F noktasında bulunan bir cismin, 1.5 F ‘de gerçek ve ters görüntüsü oluşur. Boyu ise kendi boyunun yarısıdır.
- Çukur aynada merkezde ( 2F ) ‘de bulunan bir cismin görüntüsü yine merkezde ( 2F ) , ters ve gerçektir. Boyu ise cismin boyuna eşittir.
- Çukur aynada 1,5 F noktasında bulunan bir cismin, 3F ‘de gerçek ve ters görüntüsü oluşur. Boyu ise kendi boyunun iki katıdır.
- Çukur aynanın odağındaki noktasal bir cismin görüntüsü sonsuzdadır.
- Çukur aynada 0,5F üzerinde buluna bir cismin görüntüsü ayna arkasında odak uzaklığı mesafesinde, düz ve sanaldır.
- Çukur aynanın tepe noktası üzerinde bulunan bir cismin görüntüsü yine tepe noktası üzerinde, düz, sanal ve boyu cismin boyuna eşittir.
Özel Durumlar :
1.)
2.) Bir cisim çukur aynanın odak noktasına yaklaşırken görüntüsünün boyu artar.
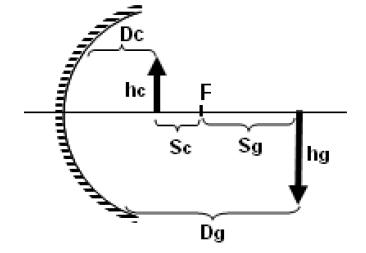
3.) Çukur aynada bir cismin görüntüsü aşağıdaki denklemlerle bulunabilir.
f : Aynanın odak uzaklığı
Hc : Cismin boyu
Hg : Görüntünün boyu
Dc : Cismin aynaya uzaklığı
Dg: Görüntünün aynaya uzaklığı
Sc : Cismin odak noktasına uzaklığı
Sg : Görüntünün odak noktasına uzaklığı
$(\begin{array}{*{20}{l}}
{\frac{{{H_C}}}{{{H_g}}} = \frac{{{D_C}}}{{{D_g}}}}\\
{ \pm \frac{1}{f} = \frac{1}{{{D_C}}} \pm \frac{1}{{{D_g}}}}\\
{{f^2} = {S_C} \cdot {S_g}}
\end{array})$
Görüntü gerçek ise işaret ( + ), sanal ise işaret ( – ) ‘dir.
4.) Bir cismin görüntüsü aynada yansıyan ışınların kesişmeleriyle oluşuyorsa görüntü gerçektir.
Eğer bir cismin görüntüsü aynada yansıyan ışınların uzantılarının kesişmesiyle oluşuyorsa sanaldır (zahiri ya da sanal ). Sanal görüntüler görülebilirken gerçek görüntüler ancak perde üzerine düşürülerek görülebilir.
TÜMSEK AYNA
Yansıtıcı yüzeyi, küre parçasının dı_ yüzeyi ise tümsek ayna yada dışbükey ayna ( konkav ayna ) denir.
Tümsek aynaların dağıtıcı özelliği vardır. Bu aynalar güneş ışınlarına dik tutulursa, yansıyan ışınların uzantıları bir noktada kesişirler. Bu noktaya aynanın odak noktası denir.
Tümsek Aynada Özel Işınlar:
- Tümsek aynaya paralel gelen ışınlar uzantısı odaktan geçecek şekilde yansır. Aynı zamanda odak doğrultusunda gelen ışınlar da paralel yansır.
- Tümsek aynanın merkezine doğru gelen ışınlar kendi üzerinden geri yansır.
- Tümsek aynanın tepe noktasına doğru gelen ışınlar asal eksenle eşit açı yapacak şekilde yansır.
- Tümsek aynaya odak noktasından gelen ışın uzantısı 0,5F’ den geçecek şekilde yansır.
- Tümsek aynaya rastgele bir ışın; normali olan merkezden gelen çizgi ile eşit açı yapacak şekilde yansır.
Yardımcı odak yardımıyla yansıyan ışının çizilmesi;
Yansıyan ışını çizmek için;
- Merkezden geçen ve gelen ışına paralel olan bir yardımcı eksen çizilir.
- Asal eksene dik olan ve odaktan geçen odak düzlemi çizilir.
- İki eksenin kesiştiği nokta, yardımcı odaktır ve yansıyan ışın bu noktadan geçer.
Tümsek Aynada Görüntü:
1.) Tümsek ayna önünde bir cisim her nerede olursa olsun görüntüsü her zaman odak ile tepe noktası
arasında oluşur. Görüntü daima düz, daima sanal ve daima cismin boyundan küçüktür.
2.) Tümsek aynada, sonsuzdaki bir cismin odak noktasında noktasal bir görüntüsü oluşur.
3.) Özel olarak tümsek aynanın odak noktasında bulunan bir cismin görüntüsü 0,5F ‘ dedir.
Özel Durumlar:
1.) Tümsek aynada görüntü daima sanal, düz ve küçüktür.
2.) Tümsek aynada; cisim aynaya yaklaştıkça görüntü boyu artar.
3.) Tümsek aynada bir cismin görüntüsü aşağıdaki formüllerle bulunabilir.

$(\begin{array}{*{20}{l}}
{\frac{{{H_c}}}{{{H_g}}} = \frac{{{D_c}}}{{{D_g}}}}\\
{ – \frac{1}{f} = \frac{1}{{{D_c}}} – \frac{1}{{{D_g}}}}\\
{{f^2} = {S_c} \cdot {S_g}}
\end{array})$







gerçekten güzel ve basit anlatılmış saçma sapan test kitaplarında (çap 10sınıf) anlayamadıgımı burda 5dk da anladım
Teşekkürler çok faydalı olmuş.
Allah razı olsun adamsınız
güzel