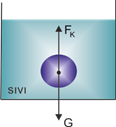
Sıvı içerisine daldırılan bir cismin sıvı tarafından yukarı doğru itilir. Yerçekimi kuvvetine zıt yönde uygulanan bu kuvvete kaldırma kuvveti adı verilir. Archimedes (Arşimet) İlkesi diye adlandırılan bu ilkeye göre, tamamı veya bir kısmı akışkana batan cisme, akışkan tarafından uygulanan kaldırma kuvvetinin büyüklüğü, cismin yer değiştirdiği akışkanın ağırlığına eşittir.
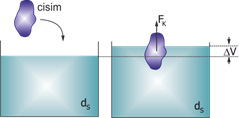
İçinde \({d_S}\) yoğunluklu sıvı bulunan şekildeki gibi bir kaba V hacimli cisim atıldığında cisme uygulanan kaldırma kuvveti yer değiştiren sıvının ağırlığı kadardır.
\({F_K} = \Delta V \cdot {d_S} \cdot g{\rm{ }} \Rightarrow \)\({\rm{ }}{F_K} = {V_b} \cdot {d_S} \cdot g\)
\(\begin{array}{l}{V_b}{\rm{ : Cismin sıvıya batan hacmi (c}}{{\rm{m}}^3}{\rm{, }}{{\rm{m}}^3}{\rm{) }}\\{{\rm{d}}_S}{\rm{ : Sıvının özkütlesi (g/c}}{{\rm{m}}^3}{\rm{, kg/}}{{\rm{m}}^3}{\rm{)}}\\{\rm{g : Yerçekimi ivmesi (m/}}{{\rm{s}}^2}{\rm{, N/kg)}}\\{{\rm{F}}_K}{\rm{ : Kaldırma Kuvveti (N)}}\end{array}\)
Sıvı içinde yüzme, askıda kalma ve batma şeklinde üç durumda bulunur. Bunları kaldırma kuvvetiyle ilişkilendirelim.
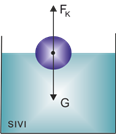
\(G > {F_K}\)
\(\begin{array}{l}G = m \cdot g{\rm{ }}{F_K} = {V_b} \cdot {d_s} \cdot g\\G > {F_K}{\rm{ }} \Rightarrow {\rm{ }}m \cdot g > {V_b} \cdot {d_s} \cdot g{\rm{ }}\\{\rm{ }}{V_c} \cdot {d_c} \cdot g > {V_b} \cdot {d_s} \cdot g\\{\rm{ }}{V_c} = {V_b}{\rm{ }}\\{\rm{ }}{{\rm{d}}_{\rm{c}}} > {d_s}\end{array}\)
Cisim batar ve tabana \({\rm{G – }}{{\rm{F}}_K}\) kadar etki yapar.
\(G = {F_K}\)
\(\begin{array}{l}G = m \cdot g{\rm{ }}{F_K} = {V_b} \cdot {d_s} \cdot g\\G = {F_K}{\rm{ }} \Rightarrow {\rm{ }}m \cdot g = {V_b} \cdot {d_s} \cdot g{\rm{ }}\\{\rm{ }}{V_c} \cdot {d_c} \cdot g = {V_b} \cdot {d_s} \cdot g\\{\rm{ }}{V_c} = {V_b}{\rm{ }}\\{\rm{ }}{{\rm{d}}_{\rm{c}}} = {d_s}{\rm{ }}\end{array}\)
Cisim, sıvı içinde asılı kalır.
\(G = {F_K}\)
\(\begin{array}{l}G = m \cdot g{\rm{ }}{F_K} = {V_b} \cdot {d_s} \cdot g\\G < {F_K}{\rm{ }} \Rightarrow {\rm{ }}m \cdot g < {V_b} \cdot {d_s} \cdot g{\rm{ }}\\{\rm{ }}{V_c} \cdot {d_c} \cdot g < {V_b} \cdot {d_s} \cdot g\\{\rm{ }}{V_c} > {V_b}{\rm{ }}\\{\rm{ }}{{\rm{d}}_{\rm{c}}} < {d_s}{\rm{ }}\end{array}\)
Cisim, sıvı içinde yüzer.
Not: Yüzen ya da askıda kalan cisimlere uygulanan kaldırma kuvveti cismin ağırlığı kadardır. Cisim dibe değiyorsa, ağırlık kaldırma kuvvetinden büyüktür.
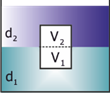
Birbirine karışmayan sıvılar içindeki cisme uygulanan kaldırma kuvveti,
\({F_K} = {V_1} \cdot {d_1} \cdot g + {V_2} \cdot {d_2} \cdot g\)
ile bulunur.
Cisimler farklı derinlikte olmalarına rağmen üçü de sıvı içinde askıda. O halde cisimlerin hepsinin öz kütlesi sıvınınkine eşittir.
\({d_1} = {d_2} = {d_3} = {d_S}\)
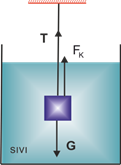
\({d_C} > {d_S}\) olması durumunda ipte
bir T gerilmesi oluşur. Bu gerilme,\(T = G – {F_K}\) şeklinde bulunur ve T’ye cismin sıvı içindeki ağırlığı denir.
*** Sıvının yoğunluğu cismin yoğunluğuna eşit ya da büyük ise \(({d_S} \ge {d_C})\), ipteki gerilme yani cismin sıvı içindeki ağırlığı sıfır(0) olur.
Cisim sıvıya bırakıldığında kaptan sıvı taşmıyorsa, cismin ve sıvının öz kütleleri ne olursa olsun, sistemin ağırlığı cismin ağırlığı kadar artar.
Taşma seviyesine kadar dolu kaba cisim atılıyor.
\({d_S} \ge {d_C}\) ise kapta ağırlaşma olmaz.
\({d_C} > {d_S}\) ise kap \(G – {F_K}\) kadar ağırlaşır.
Şekildeki sistemde cisim sıvıya daldırıldığında, kaptan sıvı taşmıyorsa;
Cismin ve sıvının öz kütleleri ne olursa olsun, sistemin ağırlığı \({F_K}\) kadar artar.
Şekildeki sistemde cisim sıvıya daldırıldığında;
cismin ve sıvının öz kütleleri ne olursa olsun, sistemin ağırlığı değişmez.
Şekildeki sistemde cisim sıvıya daldırıldığında;
cismin ve sıvının öz kütleleri ne olursa olsun, sistemin ağırlığı değişmez.