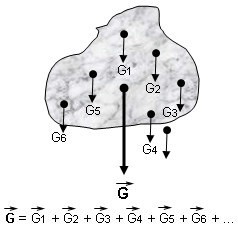
Ağırlık, cisme etkiyen yerçekimi kuvvetidir. Kütlesi m olan bir cismin ağırlığı
G=m.g
Burada g yerçekimi ivmesidir.
Ağırlık merkezi ise cismin ağırlığının uygulama noktasıdır. Başka bir deyişle ağırlık merkezi, cismin her parçasına etkiyen yerçekimi kuvvetlerinin bileşkesinin yeridir. Ağırlık merkezi, kütle merkezi olarak da ifade edilebilir.
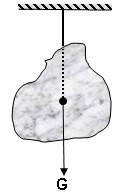
Çekim alanının olmadığı bir ortamda yalnız kütle merkezinden söz edilir. Ağırlık merkezinden asılan cisimler, nasıl asıldıysa öylece dengede kalır.
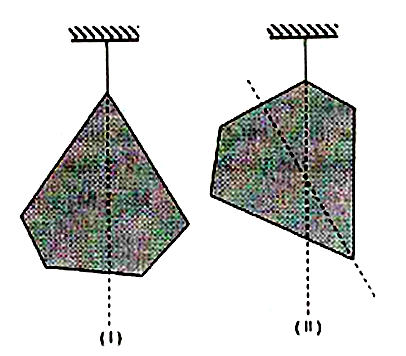
Eğer cisim herhangi bir noktasından asılırsa, asıldığı noktadan geçen düşey doğrultu ağırlık merkezinden geçecek şekilde dengelenir. Bu özellikten faydalanılarak cisimlerin ağırlık merkezleri bulunabilir. Buna göre, farklı iki noktasından asılan cismin düşey doğrultularının kesiştiği nokta ağırlık merkezi olur.
Düzgün ve türdeş cisimlerin ağırlık merkezleri geometrik merkezleridir. Düzgün ve türdeş bazı geometrik cisimlerin ağırlık merkezleri aşağıdaki gibidir.
– Bir cismin dengede kalabilmesi için ağırlık merkezinden indirilen düşey doğrultunun taban düzlemi içerisinde kalması gerekir.
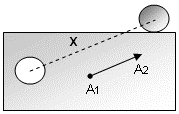
Koordinat Sisteminde Ağırlık Merkezinin Bulunması
Aynı düzlemde bulunan, birden çok cismin oluşturduğu sistemin kütle merkezinin koordinatları ise aynı yöntemle;
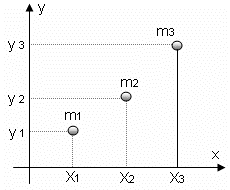
Önce ağırlık merkezi vektörünün x eksenini kestiği nokta aşağıdaki yöntemle hesaplanır.
\(x = \frac{{{m_1}{x_1} + {m_2}{x_2} + {m_3}{x_3}}}{{{m_1} + {m_2} + {m_3}}}\)
Sonra ağırlık merkezinin y eksenini kestiği nokta aşağıdaki yöntemle hesaplanır.
\(y = \frac{{{m_1}{y_1} + {m_2}{y_2} + {m_3}{y_3}}}{{{m_1} + {m_2} + {m_3}}}\)
Bu iki nokta bize ağırlık merkezinin koordinatlarını verir.
Özellikler:
1. Ağırlık merkezi problemleri “paralel kuvvet” yöntemiyle bulunur.
2. Ağırlık merkezi problemlerinde bir cismin ağırlığı verilmemişse,
– Cisim çember, çubuk veya tel ise uzunluğu,
– Levha ise alanı,
– Hacimli bir cisim ise hacmi,
ağırlığı yerine alınabilir.
3. L uzunluğundaki homojen bir telin ucundan “a” kadarlık parçası kesilerek kendi üzerine katlanırsa, ağırlık merkezi,
\(\Delta X = \frac{{{a^2}}}{L}\)
kadar yer değiştirir.
4. Homojen bir telin bir ucundan a kadarlık kısmı kesilip atılırsa kütle merkezi,
\(\Delta X = \frac{a}{2}\)
kadar yer değiştirir.
5.
Bir cismin 1/a‘lık kısmı çıkarılıp başka bir yere yapıştırılırsa ağırlık merkezi x doğrultusuna paralel olarak x/a kadar kayar.
6. Bir cismin ağırlığı, uygun şartlarda kütle ,uzunluk, alan, hacim ve yoğunlukla doğru orantılıdır.
m=d.V
Bir sistemin ağırlık merkezini bulmak için
1. Cisim kütle merkezleri bilinen parçalara ayrılır.
2. Her parçanın kütle merkezleri paralel kuvvet biçiminde çizilir.
3. Aralardaki uzaklıklar bulunur ve paralel kuvvet metoduyla bileşkenin yeri belirlenir.
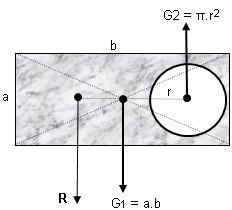
– Bir levhada eklenen parçalar, eklenen parçanın ağırlık merkezinden aşağı paralel kuvvet olarak çizilir.
– Bir levhada çıkarılan parçalar, çıkarılan parçanın ağırlık merkezinden yukarı paralel kuvvet olarak çizilir.