Seste Doppler Olayı

DOPPLER OLAYI

Sabit frekanslı ses üreten bir kaynaktan yayılan sesin, yayılması sırasında frekans değerinde bir değişiklik olmaz. Ancak ses kaynağı ya da ses algılayıcısı hareketli ise bu durum değişir. Ses kaynağının hareketli olması durumunda ya da sesi duyan kişinin hareketli olması durumunda sesin frekansı, kaynaktan çıkan frekanstan farklı olarak algılanır. Bu duruma doppler olayı denir. Doppler olayında değişen dalga boyudur. Ancak dalga boyu ile frekans ters orantılı olduğundan, gözlemci dalga kaynağının frekansını da değişmiş gibi algılar. Doppler olayı hareketli kaynağın hızının ses hızından yavaş olduğu durumlarda gözlenir. Kaynak hareket etmiyorsa dalgalar kaynak etrafında simetriktir. Frekansı f_K olan bir kaynak, özellikleri değişmeyen bir ortamda λ dalga boylu v hızıyla hareket eden dalgalar yayıyorsa;

\(\lambda = \frac{v}{{{f_k}}}\)

 

 

 

 

 

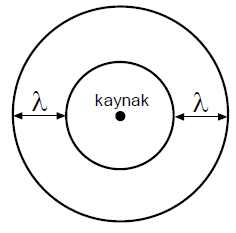
Kaynak ortama göre v_K hızıyla hareket ederse, hareket yönündeki dalgalar sıkışırken zıt yöndeki dalgalar seyrekleşir.

 

 

 

 

 

 

 

Bu durumda hareket yönünde bulunan bir gözlemcinin işittiği ses yüksek frekanslı, harekete zıt yönde bulunan gözlemcinin işittiği ses ise düşük frekanslı olacaktır.

 

 

 

 

 

 

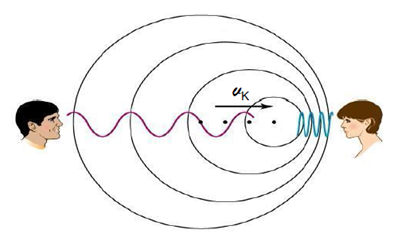
\({f_g} = {f_k}(\frac{v}{{v \mp {v_k}}})\) formülü ile işitilen sesin frekansı bulunur.

f_g : Algılanan frekans f_K : Kaynağın frekansı

v : Dalganın yayılma hızı v_K : Kaynağın hızı

Kaynak, gözlemciye doğru hareket ederse aradaki işaret (-), gözlemciden uzaklaşırsa aradaki işaret (+) alınır.

– Kaynak hareketsiz, gözlemci hareketli ve gözlemcinin hızı dalganın hızından küçük ise;

 

 

 

 

 

 

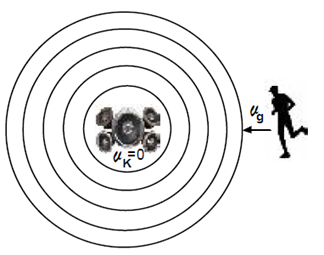
Özellikleri değişmeyen bir ortamda, f_K frekanslı, v hızıyla yayılan dalgalar üreten ve durmakta olan bir ses
kaynağına doğru vg hızıyla hareket eden bir gözlemci de
sesi farklı frekansta algılar. Algılanan bu frekans;

\({f_g} = {f_k}(1 + \frac{{{v_g}}}{v})\) ile bulunur.

f_g : Algılanan frekans f_K : Kaynağın frekansı

v : Dalganın yayılma hızı v_K : Kaynağın hızı

– Kaynak hareketsiz, gözlemci hareketli ve kaynaktan uzaklaşıyor ise;

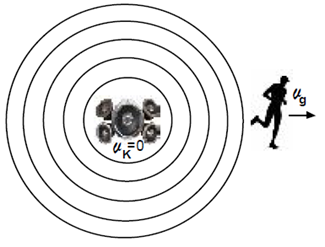
Özellikleri değişmeyen bir ortamda durmakta olan ses kaynağından v_g hızıyla uzaklaşan bir gözlemci sesin frekansını aşağıdaki formülle verildiği frekansla algılar.

\({f_g} = {f_k}(1 – \frac{{{v_g}}}{v})\) ile bulunur.

f_g : Algılanan frekans f_K : Kaynağın frekansı

v : Dalganın yayılma hızı v_K : Kaynağın hızı

– Hem kaynak hem de gözlemci hareketli ise;

Özellikleri değişmeyen bir ortamda hem ses kaynağı hem de gözlemci hareketli ise algılanan frekans aşağıdaki formülle hesaplanır.

\({f_g} = {f_k}(\frac{{v \pm {v_g}}}{{v \pm {v_k}}})\)

*Kaynak ve gözlemci arasındaki uzaklık azalıyorsa (+v_g ), (-v_K) kullanılır.

*Kaynak ve gözlemci arasındaki uzaklık artıyorsa (-v_g ), (+v_K) kullanılır.

ŞOK DALGALARI

Ses kaynağının hızı, ses hızına yaklaştığı ya da ona eşit olduğu anda ilginç bir durum ortaya çıkar.

\({f_g} = {f_k}(\frac{v}{{v – {v_k}}})\)

bağıntısına göre kaynağın hızı olan v_K, ses hızı olan v değerine eşit olursa f frekansı sonsuza gider. Yani dinleyiciye sonsuz sayıda dalga tepesi ulaşır. Kaynağın hızı ses hızından büyük olursa dalgalar kaynağın gerisinde kalır. İlerleyen bir dalga kaynağının hızı, dalgaların hızını aşarsa şok dalgaları oluşur.

 

 

 

 

 

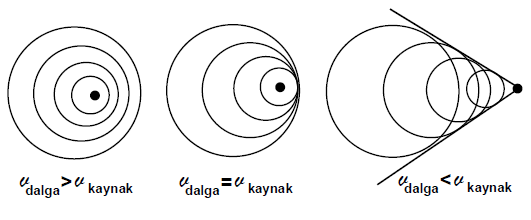
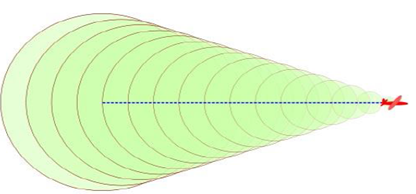
Hareket halindeki süpersonik (sesten hızlı) uçaklar, sürekli olarak yarıçapları uçağın bulunduğu konumdan dışarıya doğru büyüyen dairesel ses dalgaları oluşturur. Üst üste binen ses dalgaları moleküller üzerinde titreşim meydana getirir. Bunun sonucunda basınç oluşur. Jet uçağı ses hızına ulaştığı anda yüksek basınçlı bir hava duvarı meydana gelir. Uçaklar bu hava duvarını aştıkları anda çok şiddetli bir ses çıkarırlar. Bu olaya sonik patlama denir. Bu olaydan sonra tepesi uçağın burnunda bulunan, koni yüzeyi şeklinde büyük bir dalga oluşur. Uçak uzaklaştıktan bir süre sonra koni yüzeyi yere ulaşır ve patlama sesini andıran güçlü bir ses duyulur.